Verhalten von Kondensatoren im Gleichspannungskreis

Ein Beitrag von Günter König:
Ein Wort vorab, ich will darauf verzichten, zuviel Mathematik hierein zu bringen. Das soll nicht die Aufgabe sein. Ich denke auch, das darüber an anderer Stelle genug geschrieben wurde. Wer es will, kann in den einschlägigen Fachbüchern im Selbststudium sich mit den absoluten Feinheiten beschäftigen.

Anzeige:

Wir beginnen mit dem Kondensator, der Ladung und der Entladung. Wir schauen uns an, was bei einer Impulsförmigen Gleichspannung passiert. Und wir wollen mal schauen, ob wir den Grund herausfinden, warum ein Entstörgleis in einer digital betriebenen Anlage mehr Unheil als Gutes machen kann.

1. Testschaltung

In vorhergehenden Beiträgen über Bauelemente und Grundschaltungen wurde bereits der Kondensator und die Spule erwähnt. Wir wollen uns nun einmal mit dem Verhalten dieser Bauteile in Verbindung mit den bei unserer Modellbahn üblichen Spannungsformen befassen.

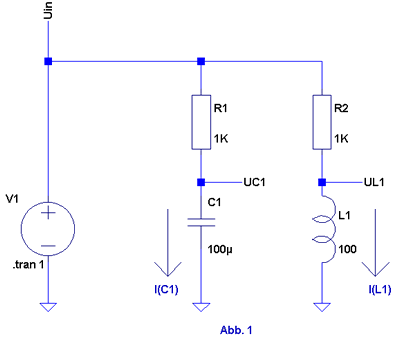
In Abb.1 ist mit V1 eine Spannungsquelle gezeichnet, die uns für die folgenden Untersuchungen die erforderliche Spannung UIN von 1 Volt liefert. Wir wollen uns im weiteren die an den Bauteilen anliegenden Spannungen ( UIN, UC1 und UL1 ) und die fließenden Ströme ( IC1 und IL1 ) durch den Kondensator und in einem zweiten Artikel durch die Spule betrachten. UC1 ist die Spannung über dem Kondensator, UL1 entsprechend die Spannung über der Spule.

2. Der Kondensator an Gleichspannung - Ladung

Beginnen wir mit der Betrachtung des Kondensators und schauen wir uns also folgendes Diagramm einmal an:

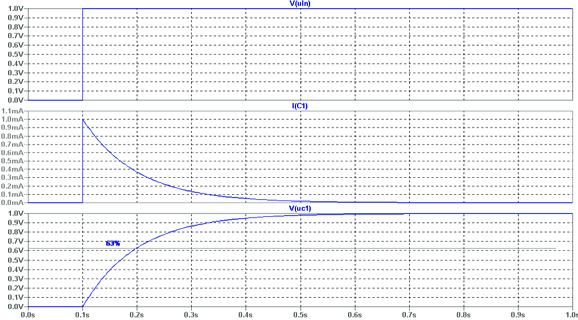
Das Diagramm setzt sich aus den drei Einzelkurvenverläufen UIN im oberen Drittel, IC1 in der Mitte und UC1 im unteren Drittel zusammen. In der waagerechten Diagrammachse ist die Zeit (hier: 1 Sekunde) eingetragen, in der senkrechten Strom und Spannung.
Was geschieht hier nun? Man sieht bei dem Verlauf UIN, das zum Zeitpunkt 0,0 s die Spannung auch 0 ist. Nach 0,1 s wird die Spannung eingeschaltet und erreicht einen Wert von 1 Volt. Der Strom hat zu diesem Zeitpunkt einen Maximalwert von 1 mA. Die Spannung am Kondensator UC1 ist zu diesem Zeitpunkt 0 Volt.
Wir haben ja schon mal was von dem sogenannten Ohmschen Gesetz gehört welches besagt, dass ein Strom durch einen elektrischen Leiter einen Spannungsabfall hervorruft. Hier ist aber die Spannung über dem Kondensator gleich 0 Volt, was den Schluss nahelegt, dass hier der Widerstand gleich 0 Ohm sein muss - dies bedeutet aber letztlich ein Kurzschluss.
Wenn wir weiter überlegen, sehen wir das die Eingangsspannung 1 Volt und der Strom 1mA beträgt. Errechnen wir hieraus den Widerstand nach dem Ohmschen Gesetz so erhalten wir einen Wert von 1 kOhm. Und genau dies ist ja der Wert von R1.

Man kann also sagen: Im Einschaltmoment wird der Strom durch den Vorwiderstand R1 begrenzt.
Oder anders: Im Einschaltmoment ist der Strom durch den Kondensator theoretisch unendlich hoch da der Widerstand gleich 0 Ohm ist.

Ein Satz zum Merken:
Kondensator - Strom eilt vor

Wir sehen nun weiter, das der Strom IC1 abnimmt und die Spannung über dem Kondensator langsam ansteigt. Dieser Vorgang führt irgendwann dazu, dass die Spannung über dem Kondensator gleich der Spannung UIN und der Strom IC1 gleich 0 mA sein wird. Würden wir jetzt den Kondensator abklemmen und an seinen Anschlüssen ein Voltmeter anlegen, sehen wir, dass die angezeigte Spannung 1 Volt beträgt. Man sagt, der Kondensator ist geladen.
Dieser Verlauf der Ladung (der Kurvenverlauf) ist den Kondensatoren eigen. Sie ist bei allen Kondensatoren identisch und unterscheidet sich nur im zeitlichen Verhalten. Welches nichts weiter bedeutet, das ein Kondensator mit einer hohen Kapazität einen längeren Zeitraum zur Ladung benötigt als einer mit einer kleinen Kapazität.
Gibt es eine Möglichkeit, diesen Vorgang zu berechnen? Ja, gibt es. Man hat hierfür den Begriff "Zeitkonstante" eingeführt. Man bezeichnet die Zeitkonstante mit dem griechischen Buchstaben Tau.
Dieser wert errechnet sich aus dem Vorwiderstand und der Kapazität
Tau = R * C (Zeit in Sekunden, Widerstand in Ohm, Kapazität in Farad)

Diese Zeit beschreibt den Punkt auf der Ladekurve für UC1 wann die Spannung auf 63 % der Eingangsspannung UIN angestiegen ist. Rechnen wir mal,

1 kOhm = 1000 Ohm,
100 µF = 0,0001 Farad

Tau = 1000 * 0,0001 = 0,1 Sekunden.

Schauen wir noch mal in das Diagramm sehen wir tatsächlich, das 0,1 Sekunde nach Beginn der Ladung (bei 0,2 Sekunden) die Spannung auf 0,63 Volt angestiegen ist.
Eine Eigenheit dieses Kurvenverlaufs ist, dass er nicht linear ist. Das heißt, die Spannung ist nach der doppelten Zeit nicht doppelt so hoch. Wir haben es hier mit einer sogenannten e-Funktion zu tun. Nichtsdestotrotz können wir es aber berechnen.

Beispiel: Wir wollen wissen, wie hoch die Spannung UC1 zum Zeitpunkt 0,4 Sekunden ist und welcher Strom IC1 dann noch fließt.

Hierfür gibt es folgende Rechengrundlage:
UC1 = UIN * (1-e^-(t/Tau)), wobei t der gewünschte Zeitpunkt und Tau die Zeitkonstante ist. Auf dem Taschenrechner ist die e-Funktion meist über die Taste ex zu finden. Bei "e" handelt es sich um eine mathematische Konstante, ähnlich "Pi". Als Näherungswert können wir 2,71828 einsetzen.

Aber gut, tippen wir mal ein:

1 * (1-e^{-(0,3 / 0,1)}) und erhalten als Ergebnis 0,950 Volt.

Der Strom zu diesem Zeitpunkt errechnet sich aus

IC = UIN/R1 * e^-(T/Tau) ergibt einen Strom von ca. 0,05 mA.
(Der Term UIN/R1 beschreibt den maximal möglichen Strom IC1)

Schauen wir mal ins Diagramm, werden wir diese Ergebnisse an entsprechender Stelle recht genau wiederfinden.

Nun denn, nach kurzen mathematischen Auswucherungen beschäftigen wir uns noch mit dem Entladevorgang, denn was geladen wurde, kann auch wieder entladen werden.

3. Der Kondensator an Gleichspannung - Entladung

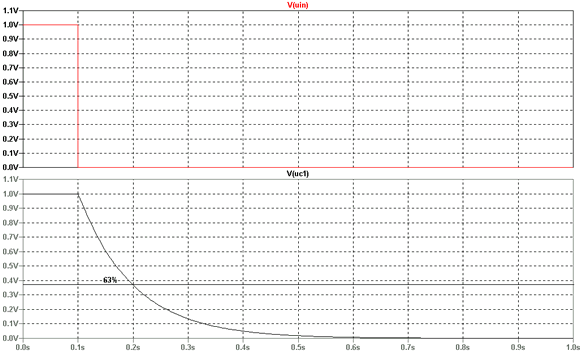
Schauen wir wieder auf das Diagramm ist im oberen Teil die Eingangsspannung und unten die Spannung am Kondensator eingezeichnet. Wir sehen, das nach 0,1 Sekunden die Eingangsspannung abgeschaltet wird und die Spannung am Kondensator nach der uns nun bekannten e-Funktion sinkt.
Die Berechnungen sind genauso wie bei der Ladung - nur ist die Zeitkonstante auf den Wert der Kondensatorendspannung bezogen. Es heißt also jetzt, Tau ist der Zeitpunkt, auf den der Wert der Kondensatorendspannung um 63 % abgefallen ist. Das sollten in unserem Beispiel 100 mS nach dem Abschalten noch 0,37 V sein. Aber rechnen wir noch mal nach

UC = UC1 * e^-(T/Tau) und erhalten als Wert 0,36787 Volt.
(UC = Spannung zum Zeitpunkt T, UC1 = Ladeentspannung)

Für den Verlauf des Entladestromes gilt folgendes: Im ersten Moment des Abschaltens erreicht der Entladestrom einen Maximalwert um dann nach der e-Funktion abzufallen. Der Strom zum beliebigem Zeitpunkt T errechnet sich aus:

IC = UC1/R1 * e^-(T/Tau)
(IC = Strom zum Zeitpunkt T, UC1 = Ladeentspannung)
(Der Term UC1/R1 beschreibt den maximal mögliche Entladestrom IC1)

4. Der Kondensator an impulsförmiger Gleichspannung

Die bisher verwendete Spannungsquelle liefert uns nun eine Impulsförmige Gleichspannung mit einer Impulsdauer von 0,5 sec.

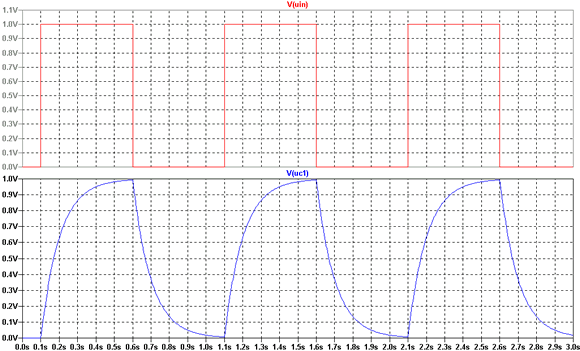
Der obere Kurvenverlauf zeigt dies deutlich: Der Impuls wird nach 0,1 Sekunde eingeschaltet und endet nach 0,6 Sekunden. Das ganze geschieht dreimal sodas wir drei Impulse sehen. In der unteren Kurve sehen wir nun die Spannung am Kondensator mit seinen Lade- und Entladekurvenverläufen.
Aufgrund unserer Dimensionierung mit R1 = 1 kohm, C1 = 100 µF und der Impulsdauer von 0,5 Sekunden sieht es so aus, als würde der Kondensator immer bis auf die Eingangsspannung aufgeladen und bis auf 0 Volt entladen.
Nur, mit unserer Eingangskurvenform hat unsere Spannung am Kondensator nur noch wenig gemein. Wir sehen, irgendwie wird unser sauberer Rechteckimpuls ganz schön verbogen.

Als nächstes ändern wir mal die Impulsdauer, wir werden ihn mal nur 0,05 Sekunden dauern lassen. Die Werte für R1 und C1 bleiben gleich.

Was könnte passieren?

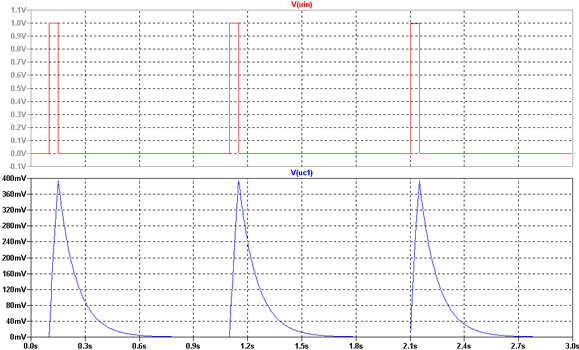
Nun, es fällt sofort auf, das die Ladeendspannung gar nicht mehr die Eingangsspannung erreicht. Sie erreicht nur einen Wert von ca. 400 mV!

Verkürzen wir nochmals die Impulsdauer auf einen Wert von 5 mSekunden.

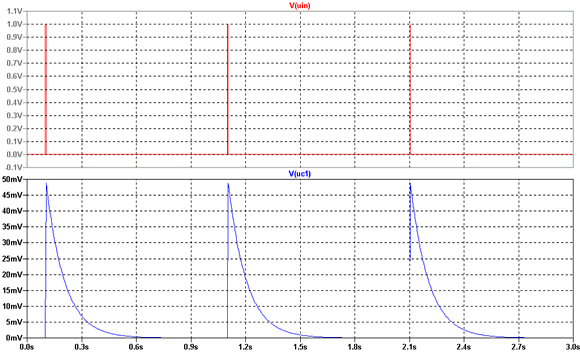
Die Ladeendspannung erreicht nun noch nicht mal den Wert von 50 mV!

Kann uns diese Erscheinung nützen?
Ja, wenn wir eine MoBa mit einer reinen Gleichspannung betreiben, entstehen durch Kollektormotoren zwangsläufig Störungen, die sich durchaus unangehm in Nachbars Radio oder Fernseher bemerkbar machen. Da diese Störungen aus sehr kurzen Impulsen bestehen, können wir sie mit einem Kondensator bedämpfen. Und genau das wird über ein sogenanntes Entstörgleis erreicht.
Oft befinden sich in der Lok aber echte Entstörglieder bestehend aus einer Kombination von Spulen und Kondensatoren die insofern wirkungsvoller sind, da sie die entstehenden Störungen direkt „vor Ort“ unterdrücken. Wie das genau wirkt, werden wir in Zusammenhang mit der Spule (Beitrag erscheint demnächst) noch etwas genauer besprechen.

5. Spannungsversorgung einer digitalen Modellbahn (DCC)

Bei einer rein Gleichspannungsmäßig gesteuerten Modellbahn wird die über das Gleisnetz zugeführte Gleichspannung direkt zu Steuerung der Motoren und Beleuchtung benutzt. In einer digital gesteuerten Anlage ist das anders. Irgendwie muss die Energie für die Motoren, Beleuchtung usw. übertragen werden wie auch Daten, um den Motor usw. zu steuern. Dies geschieht auch über eine Spannung. Schauen wir uns mal solche eine Spannung mal an:

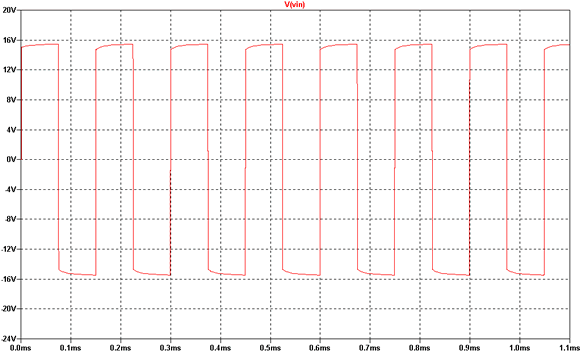
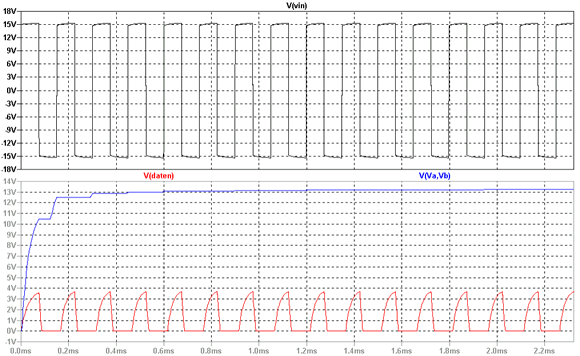
Was ist nun besonderes daran? Auf dem ersten Blick sieht es aus wie eine impulsförmige Gleichspannung, bei näherem hinsehen erkennen wir, das die Spannung aber einen positiven Höchstwert (ca. +16 V) und einen negativen Höchstwert (ca. -16 V) hat. Es handelt sich also um eine impulsförmige Wechselspannung. Es wird also letztlich eine Wechselspannung unseren Gleichspannungsloks zugeführt. Was geschieht nun in der Lok mit dieser Wechselspannung?

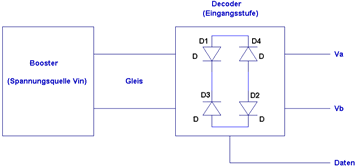
Sie wird einem Decoder zugeführt, der erstmal die Vorsorgungsspannung generieren muß damit der Decoder überhaupt arbeiten kann. Aus der Wechselspannung muss also erstmal eine Gleichspannung erzeugt werden. Schematisch einmal dargestellt:

An den Punkten Va und Vb erhalten wir unsere Gleichspannung und am Ausgang "Daten" eben die Daten. An Va und Vb bekommen wir durch Gleichrichtung eine recht saubere Gleichspannung, die weiter verarbeitet werden kann. In rot sehen wir die Datenfolge. Wie jetzt die Daten behandelt werden, ist an dieser Stelle nicht wichtig. Nur soviel, es kommt auf einen möglichst sauberen Impuls mit ausgeprägten steilen Flanken und einem entsprechendem Pegel an.

Wir wollen uns nun wieder unserem Kondensator widmen, die Frage war: was kann ein Entstörgleis anrichten? Wie wirkt sich das aus?

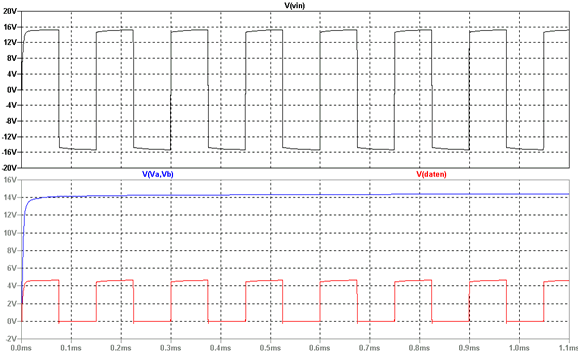
In der oberen Diagrammhälfte ist wieder die Eingangsspannung dargestellt. Unten die Eingangsspannung und die Daten. Wir sehen, das die erforderliche Gleichspannung einen anderen Verlauf hat. Dies ist aber nicht so tragisch, viel schlimmer ist die Verfälschung der einzelnen Datenimpulse. Von sauberen Flanken kann hier nicht mehr die Rede sein. Ein digitales System reagiert dann unweigerlich mit Ausfällen. Es ist durchaus schon vorgekommen, das nach einem Umbau Analog -> Digital nichts mehr funktionierte weil an irgendeiner Stelle ein Entstörgleis vergessen wurde auszubauen.

Das Verhalten von Spannung und Stom bei Spulen/Induktivitäten wird unter "Spulen" näher beleuchtet.

Danke an Günter König für den Artikel.