Verhalten von Spulen / Induktivitäten

Ein Beitrag von Günter König.
Dieser Artikel ist die Fortsetzung der Betrachtung über das Verhalten von Kondensatoren.

Anzeige:

Zur Erinnerung noch mal der Messaufbau:

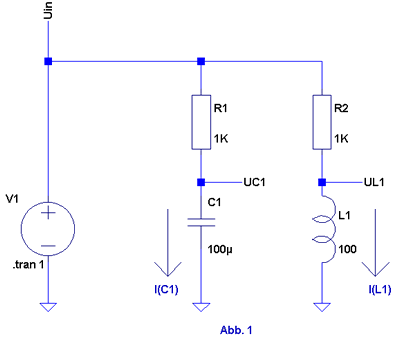
1. Die Spule an Gleichspannung - Einschaltvorgang

Für die weiteren Erklärungen betrachten wir nun den Widerstand R2, die Spule L1 und deren Spannung UL1 sowie den Strom IL1.
Wir beginnen mit dem Einschaltverhalten einer Induktivität und schauen auf das entstehende Diagramm:


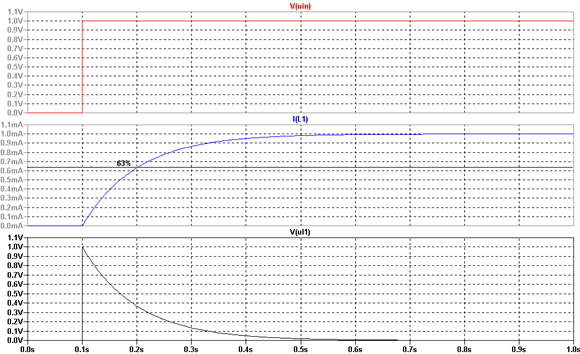
Im oberen Drittel des Diagramms haben wir wieder die Eingangsspannung eingetragen, in der Mitte den Strom IL1 und unten die Spannung UL1.

Versuchen wir, die Kurven zu deuten:
Unmittelbar nach dem Einschalten zeigt uns die Spannung UL1 einen Maximalwert während der Strom IL1 bei 0 liegt. Die Spannung UL1 ist hier gleich der Eingangsspannung. Wenn aber dann der Strom IL1 gleich 0 ist bedeutet das doch, das der Widerstand unendlich hoch sein muss.
Im Einschaltmoment ist der Strom durch die Spule theoretisch = 0 da der Widerstand = unendlich hoch ist.

Als „Eselsbrücke“ für den Stromverlauf können wir uns merken:
Induktivität - Strom kommt zu spät!

Im weiteren Verlauf steigt der Strom nach der e-Funktion auf seinen Höchstwert an, der durch die Größe des Widerstandes R2 bestimmt wird und in diesem Falle bei 1 mA liegt. Ein Maß für den zeitlichen Verlauf des Stromanstiegs wird durch das Verhältnis L/R bestimmt und wieder als Zeitkonstante Tau bezeichnet:

Tau = L / R (Sekunden, Ohm, Henry)

und bestimmt den Punkt, wo der Strom auf 63 % seines Maximalwertes angestiegen ist. Mit unserer Dimensionierung R = 1 kOhm und 100 Henry erhalten wir für Tau: 100 / 1000 = 0,1 Sekunden. Was also wieder heißt, das bei 0,2 Sekunden (0,1 Sekunden nach dem Einschalten) 63 % des Maximalstroms erreicht werden. Wie beim Kondensator die Maximalspannung nach ca. 5 Tau erreicht wird, ist es hier mit dem Strom. Für die Berechnung des Stromes nach einer beliebigen Zeit können wir folgende Formel benutzen:

IL = UIN/R2 * (1-e^-(T/Tau)) [Ampere, Volt, Ohm, Sekunden]

Wobei sich aus UIN/R2 der maximal erreichbare Strom errechnet.
Beispiel: Wir wollen den Strom nach 5 Tau errechnen also nach 0,6 Sekunden. Für Tau haben wir 0,1 Sekunden errechnet, demnach sind 5 Tau = 0,5 Sekunden. Setzen wir also ein:
(1/1000)*(1-e-^(0,5/0,1)) = 0,993262 mA
Schauen wir auf die Stromkurve im Diagramm, stellen wir fest: Stimmt auffallend!!

So, wir wollen jetzt mal die Werte unserer Spule ändern und auch den Widerstand anders dimensionieren. Setzen wir mal für die Spule einen Wert von 2,2 Henry ein und als Widerstand R2 nehmen wir einen Wert von 22 kOhm. Unsere Spannungsquelle liefert uns eine Spannung UIN von 1 Volt. Wir wollen nun wissen, wie hoch der Strom IL1 nach Tau und nach 3 Tau ist. Wie gehen wir vor?
Berechnen wir als erstes den maximalen Strom
I = UIN/R2 = 1 / 22000 = 0,00004545 Ampere oder 0,04545 mAmpere (mA) oder 45,45 µAmpere (µA)

Nun berechnen wir Tau nach L/R = 2,2/22000 = 0,0001 Sekunden. Dies entspricht einer Zeit von 100 µSekunden (µS). Demnach sind 3 Tau = 300 µS. Da wir in diesem Falle einmal T = Tau = 100 µS und im zweiten Fall T = 3 Tau = 300 µS ist es einfach. Als erste Ergebnisse haben wir nun:
IL1 = 45,45 µA
T = 100 µS
T2 = 300 µS

Rechnen wir weiter:
IL(Tau) = IL1 * (1 - e ^-(T/Tau)) = 0,00004545 * (1 - e ^{-(0,0001 /0,0001)}) = 0,00002873 mA
Dies entspricht einem Strom von = 28,7µA

Für den zweiten Zeitpunkt ersetzen wir nur die Zeit T in obiger Formel:
IL(Tau) = IL1 * (1 - e ^-(T/Tau)) = 0,00004545 * (1 - e ^{-(0,0003 / 0,0001)}) = 0,000043187 A
Dies entspricht einem Strom von = 43,19 µA

Fassen wir jetzt die Ergebnisse zusammen:
Nach 100 µS beträgt der Strom durch die Spule 28,7 µA und ist nach 300 µS auf einen Wert von 43,10 µA angestiegen. Zur Kontrolle sehen wir uns nochmal das Diagramm für diese Werte an und vergleichen die Realität mit unseren Ergebnissen (Dieses und wie alle anderen Diagramme wurden übrigends mit einem Spice Simulationsprogramm erstellt).

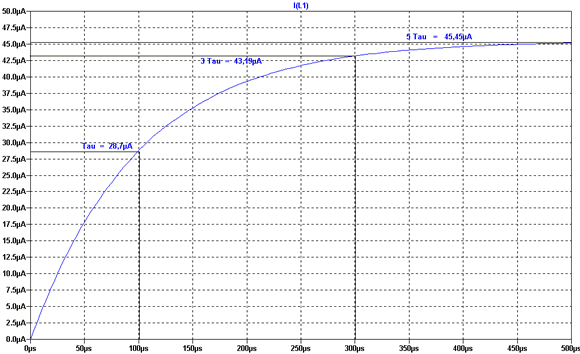
Was wissen wir nun wenn wir unsere Ergebnisse mit dem Diagramm vergleichen?

1. Wir haben richtig gerechnet (hoffentlich).
2. Der Stromverlauf bei der Spule entspricht dem Spannungsverlauf beim Kondensator.
3. Der Spannungsverlauf der Spule entspricht dem Stromverlauf beim Kondensator.
4. Der zeitliche Verlauf des Stromes ist abhängig von der Dimensionierung von R und L.

Ob die Spule eine zugeführte Spannung wie ein Kondensator speichern kann, können wir zur Zeit noch nicht feststellen. Aber wir haben doch Energie zugeführt, es floss ein Strom und eine Spannung lag auch an... Bringen wir Licht ins Dunkle und schauen uns eine der interessantesten Erscheinungen in der Elektrophysik an:

2. Die Spule an Gleichspannung - Ausschaltvorgang

Wir nehmen zur Betrachtung wieder die alten Werte mit R2 = 1 kOhm und L1 = 100 H. Weiters nehmen wir an, das unsere Spannungsquelle wieder eine Spannung von 1 Volt abgibt. Nach 100mS schalten wir dann die Spannung ab. Was passiert? Werfen wir einen Blick auf das Diagramm:


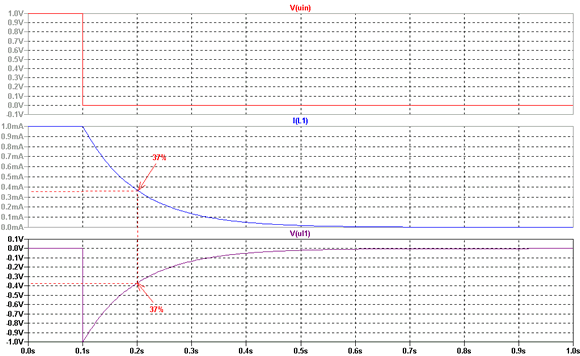
Im oberen Drittel sieht man, wie nach 0,1 Sekunde die Spannungsquelle abgeschaltet wird, also auf 0 Volt zurück geht. Man kann sehen, dass bis jetzt ein Strom von 1 mA geflossen ist.
Aber nach dem Abschalten fließt weiterhin Strom. Er nimmt zwar wieder nach der e-Funktion ab, aber es fließt ein Strom.
Was ist mit der Spannung? Als die Spannungsquelle eingeschaltet war, lag sie bei 0 Volt. Jetzt, unmittelbar nach dem Abschalten liegt sie bei - 1 Volt. Wie ist denn das zu erklären? Wurde da etwa doch irgendwas gespeichert?

Jetzt müssen wir aber doch etwas weiter ausholen: Also, fließt ein Gleichstrom durch eine Spule bauen sich um die Spule herum magnetische Feldlinien auf. Das lässt sich mittels eines Kompasses in unmittelbarer Nähe der Spule beweisen: Wird die Spannung eingeschaltet, wird auch die Kompassnadel ausgelenkt. Unmittelbar nach dem Abschalten sind diese Feldlinien noch stabil vorhanden. Da aber nun kein Strom mehr fließt um das Magnetfeld aufrecht zu erhalten, fallen die Feldlinien zusammen und erzeugen aber nun in der Spule eine Spannung. Man sagt, sie induzieren eine Spannung. Charakteristisch für diese Spannung ist, dass sie der angelegten Spannung entgegen wirkt.

Diesen Vorgang bezeichnet man als „Selbstinduktion“!
Die entstehende Spannung nennt man „Selbstinduktionsspannung“!

Wie man also sieht, wurde wohl doch etwas gespeichert. Bei der Spule ist es so, das die zugeführte Energie in einem magnetischem Feld gespeichert wird und beim Abschaltvorgang wird nun diese gespeicherte Energie wieder abgegeben. In unserer Testschaltung wird die Spule über die Spannungsquelle und dem Vorwiderstand geladen. Entladen wird sie über dem Vorwiderstand und der Spannungsquelle. Daher sehen die Lade- und Entladekurven auch von den Werten her identisch aus.

3. Die Selbstinduktion bei unterschiedlicher Ladung - Entladung

Im Normalbetrieb verläuft die Ladung / Entladung aber nicht gleich. Denken wir doch an ein Relais: Das wird über einen Schalter an Betriebsspannung gelegt und eingeschaltet. Anschließend öffnen wir den Schalter und das Relais fällt ab. Wie sieht denn dann die Entladung aus? Um das festzustellen, fügen wir in unserer Testschaltung einen Schalter ein und bezeichnen ihn mit "S".


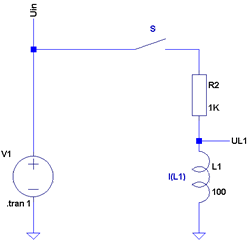
Wir schalten die Spannungsquelle ein und schließen den Schalter. Das Magnetfeld wird nun aufgebaut. Währenddessen machen wir uns noch ein paar Vorgedanken über die Zeitkonstante der Schaltung mit dem Schalter. Beim Laden liegen der Kontaktwiderstand des Schalters und der Vorwiderstand in Reihe zur Spule. Der Widerstand des Schalters ist gering, im Bereich von ca. 0,001 Ohm. Danach ist die Zeitkonstante
Tau = L / (R2 + RSchalter) 100 / (1000 + 0,001) = 99,99999 mS

Ist der Schalter geöffnet, wird der Widerstand des Schalters sehr hochohmig. Er liegt dann bei mehreren 1000 MOhm.
Die Zeitkonstante ist bei angenommenen 2000 MOhm: 100 / (1000 + 2000E6 Ohm) = 0,5 µS

Das heißt, die Entladung findet sehr schnell statt und durch die schnelle Änderung des Magnetfeldes wird eine hohe Spannung induziert. Mit anderen Worten, die entstehende Abschaltspannung (Selbstinduktionsspannung) ist sehr hoch! Betrachten wir uns das Ganze mal in einer immer wieder vorkommenden Schaltstufe, einer Relaisschaltung:



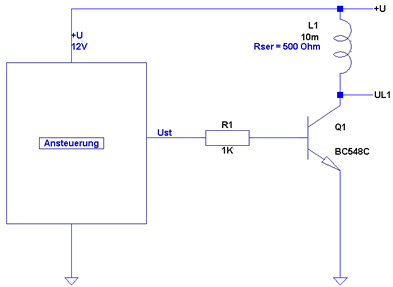
In der Box "Ansteuerung" steckt irgendeine Auswerteschaltung, die uns die Spannung UST für den Schalttranstor Q1 zur Verfügung stellt. Die Spannung +U ist die Betriebsspannung für die Relaisstufe. Wir gehen davon aus, dass die Ansteuerung eine Spannung bereitgestellt hat so das unser Relais angezogen ist. Nach 2 mS schaltet das Relais ab. Wir messen an den Punkten +U und UL1 . Betrachten wir das Diagramm:



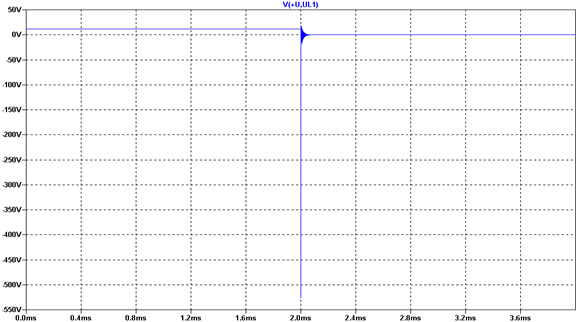
Man sieht, dass nach zwei Millisekunden eine recht hohe aber sehr kurze, negative Spannungsspitze von knappen -550 V auftaucht. Diese durch Selbstinduktion entstehende Spitze muss unbedingt vermieden werden, da sie absolut zerstörerisch auf Halbleiterbauelemente wirkt. Anders gesagt: Das knallt nur noch und danach ist Schluss mit lustig! Es gilt also zu verhindern, das so etwas passiert. In der Praxis ist das relativ einfach gelöst, indem man eine Diode mit entsprechender Belastbarkeit in Sperrichtung parallel zur Relaisspule schaltet. Das sieht dann folgendermaßen aus:



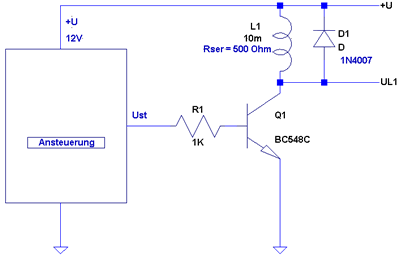
Wiederholen wir den Schaltvorgang nun nochmals, wird die Sache wesentlich besser:


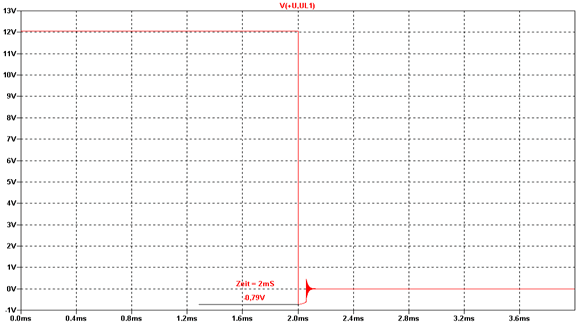
Nach 2 mS wird abgeschaltet und die im vorangegangenen Beispiel so hohe Spannungsspitze ist auf einen Wert von knapp -0,8 V zusammengefallen. Das liegt nun daran, das die Selbstinduktionsspannung an dem Punkt UL1 positiver als die Spannung an +U ist. Die Diode ist nur in diesem Falle leitend und begrenzt die Induktionsspannung auf einen absolut ungefährlichen Wert (gleich der "Schwellspannung" der Diode) und schützt so die Halbleiterschaltkreise. Im normalen Betrieb liegt die Diode in Sperrichtung, da die Spannung an +U positiver als an UL1 ist.

Man nennt eine Diode parallel zu einer Induktivität (Relaisspule, Weichenspulen bei Gleichspannungsbetrieb etc.) auch "Freilaufdiode".

Dies war ein praktisches Beispiel zur Selbstinduktion ganz ohne Rechnerei. Vielleicht ist ja jetzt so manchem (mancher) klar geworden, warum bei ihm (ihr) einige Bauteile immer scheinbar grundlos sterben. Für den praktischen Einsatz ist der angegebene Diodentyp 1N4007 in der Regel gut geeignet. Oft reichen aber auch Typen wie 1N4148 aus. Dies ist aber abhängig von den verwendeten Relais. Gibt es keinerlei Daten über den seriellen Innenwiderstand oder die Induktivität der Relaisspule, sollte immer 4007er Diode gewählt werden.

Auf eine weitergehende Betrachtung der Selbstinduktion und auf mögliche Berechnungen wollen wir aber nicht mehr eingehen - dies würde ich zwar gerne machen, es würde aber mit Sicherheit den Rahmen des Ganzen sprengen.


Danke an Günter König für den Artikel.

Das sagen User zu diesem Thema (die letzten 5 Beiträge, 6 Beiträge insgesamt):